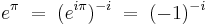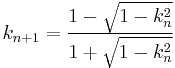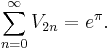Gelfond's constant

In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that

e^\pi \; = \; (e^{i\pi})^{-i} \; = \;(-1)^{-i}

where i is the imaginary unit. Since −i is algebraic, but certainly not rational, eπ is transcendental. The constant was mentioned in Hilbert's seventh problem. A related constant is 2^\sqrt{2}, known as the Gelfond–Schneider constant. The related value π + eπ is also irrational.[1]

Contents

Numerical value

The decimal expansion of Gelfond's constant begins

e^\pi \approx 23.14069263277926\dots\,.

If one defines 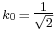\scriptstyle k_0\,=\,\tfrac{1}{\sqrt{2}} and

k_{n%2B1}=\frac{1-\sqrt{1-k_n^2}}{1%2B\sqrt{1-k_n^2}}

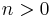for n > 0 then the sequence[2]

(4/k_{n%2B1})^{2^{-n}}

converges rapidly to e^\pi.

Geometric peculiarity

The volume of the n-dimensional ball (or n-ball), is given by:

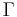V_n={\pi^\frac{n}{2}R^n\over\Gamma(\frac{n}{2} %2B 1)}.

where R is its radius and \Gamma is the gamma function. Any even-dimensional unit ball has volume:

V_{2n}=\frac{\pi^n}{n!}\

and, summing up all the unit-ball volumes of even-dimension gives:[3]

\sum_{n=0}^\infty V_{2n} = e^\pi. \,

References

  1. ^ Nesterenko, Y (1996). "Modular Functions and Transcendence Problems". Comptes rendus de l'Académie des sciences Série 1 322 (10): 909–914. 
  2. ^ Borwein, J. and Bailey, D. (2003). Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters. p. 137. 
  3. ^ Connolly, Francis. University of Notre Dame

External links